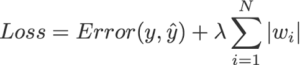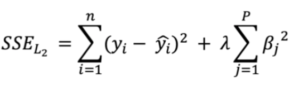The Lasso regression is a regularization technique and a type of regression that is well-suited for models showing high levels of multicollinearity. It is also known as the L1 regularization technique. This technique is often used when there is a high number of features present in the dataset, as this technique can automatically perform feature selection. [Read More]

The full form of the word “LASSO” means Least Absolute Shrinkage and Selection Operator.

Regularization is an important concept used to avoid over-fitting the data, especially where the trained and test data vary. This technique is implemented by adding a penalty term to the best fir line derived from the model trained on training data. By doing this, we can achieve lesser variance in the test data.

In the above image, we can see that the loss function is a sum of 2 terms, the error term and the penalty term L1. The error term can be any loss function for the regression problem like mean absolute error, mean squared error, r2 score, etc. The penalty term is an absolute value of weight Wi and the Lambda is a coefficient multiplied by the penalty term L1.

Table of Content

The Reason Behind Spasity
Case 1: Ridge Regression
Case 2: Lasso Regression
3 Different Conditions For Values of “m” in Lasso Regression
Conclusion
References

The Reason Behind Sparsity

In the case of Simple Linear Regression, the formula for the best-fit line was

y = mx + b

where m is the slope of the best fit line and the term b is the y-axis intercept. So from the equation of y, we can derive that:

b = y^ - mx^

where,y^ = mean of y values

x^ = mean of x values

from the statistical solutions, we can derive the formula for m which stand to be

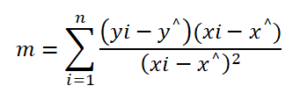
Case 1: Ridge Regression

In the case of Ridge or L2 regression, the formula of the loss function will be the same as the normal loss function but with the additional penalty term L2.

Image Source

Where SSE = Squared Sum Error

If we modify this equation and try to get the formula for the slope m using statistical methods the formula will be the same as simple linear regression slope formula with an additional term lambda in the denominator.

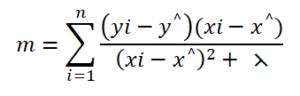
Now here in the case of ridge regression, to make the value of slope m to be zero, the term in the numerator should be zero, so here no matter how big or small the value of lambda is, it will not affect the value of m to be zero. So the value of slope m will always reach near values of zero but not the exact zero value.

Case 2: Lasso Regression

In the case of Lasso or L1 regression, the formula for the slope m will be different for 3 different values of m, which is for

m greater than zero.
m less than zero.
m equal to zero.

1. For `m` > 0:

when the value of m will be greater than zero it means that the term in the numerator will also be greater than zero. so now if we increase the values of lambda to some extent simply the value of the numerator in the equation will decrease, now after increasing the values of lambda, when the values of lambda will be equal to the other term in the numerator the difference will be zero and the values of m will be zero, but as we discussed for the zero value of m we have a different equation to follow. so the values will reach zero but they will not be negative as after reaching to zero value of m we have to follow another equation.

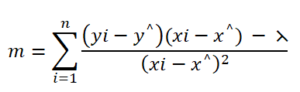
2. For `m` < 0:

In the case where the values of m will be less than zero, we have different equations to follow. same as the above case if we start increasing the value of lambda which is added in the numerator term, and if the other term in the numerator is negative then to some value of lambda the sum of these two terms will be negative, but after increasing the value of lambda the numerator term will start increasing and reached to zero, so it will reach to zero value but after reaching zero value this same equation will not be followed and then there will not be any reading after zero.

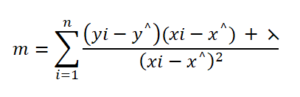
3. For `m` = 0:

In the case of m equals zero we have the same equation as simple linear regression slope formula. which will be followed if the value of m reached zero.

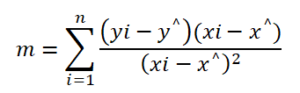
Let’s try to understand the same thing with the help of an example dataset. In both cases, we can apply ridge and lasso regression and analyze the values with the description of the features.

In the case of ridge regression, different features can have high negative or positive values but as the value of alpha or lambda increases the values tend to be reach near zero but do not attain the exact zero values.

Image Source

If we try to apply the lasso regression to the same dataset and try to plot the table for that, the values of different features are having high positive or negative values, but as the value of alpha or lambda increases the values start reaching the exact zero value but not more or less than that as after reaching zero, it will follow another equation for the suitable situation of m being positive or negative.

Conclusion

In this article, we first understood the basic concept of ridge and lasso regression and their respective formulas for loss and slope functions. The reasons why lasso regression creates sparsity are discussed institutionally with mathematical formulas. Understanding these key concepts will help one to understand the reason and the core math behind the ridge and lasso regression and their behaviour to create sparsity or not.

Some Key Insights from this article are:

The Ridge and Lasso regressions are the regularization techniques used for many purposes. (e.g avoid over-fitting, feature selection, etc.)
The loss functions for ridge and lasso regression are attained by adding the penalty term L2 and L1 respectively to the normal loss function.
The ridge regression does not crease sparsity as the lambda term in the denominator will not affect the value of the term in the numerator and hence the value of slope m.
Lasso regression creates sparsity in the dataset as there is a lambda term added or subtracted for different values of slope m and when the value of m reached zero but does not cross zero value.

References

[1] https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Lasso.html
[2] https://jamesmccaffrey.wordpress.com/2022/10/21/lasso-regression-from-scratch-using-python/
[3] https://hands-on.cloud/implementation-of-ridge-and-lasso-regression-using-python/
[4] https://www.delftstack.com/howto/python/lasso-regression-in-python/
[5] https://you.com/search?q=lasso%20regression%20implementation%20python