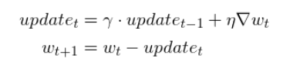Nesterov Accelerated Gradient (NAG) Optimizer in Deep Learning


data science machine learning

Parth Shukla

Ml wizard


In deep learning, optimizers are the type of function which are used to adjust the parameters of the model. The optimizers are used in deep learning to adjust the weights and biases of the neural networks and reduce the overall loss from the model to achieve higher accuracy. There are many types of optimizers used in deep learning to adjust the best weights and biases for the model in terms of overall loss.

Mostly used optimizers are gradient descent and its 3 types are batch, stochastic, and mini-batch, due to the slow training and high computation power with normal gradient descent there was a need for some advanced optimizers and back then scientists came with momentum optimizers which were faster than gradient descent and work on the concept of momentum, which works as a momentum or velocity while training the model on the desired data.

Nesterov accelerated gradient optimizer is an optimizer that is an upgraded version of momentum optimizers and mostly it performs well than momentum optimizers.

Table of Content

  1. The Need for Nag Optimizer
  2. The Mathematics Behind Nag
  3. Why Nag is Faster?
  4. Implementation of Nag: Code
  5. Conclusion
  6. References

The Need for Nag Optimizer

Although the momentum optimizer was fast and more accurate than gradient descent, in some datasets it tends to perform slowly and converges slowly. Changing the value of the decay factor or beta in the momentum optimizer can achieve higher accuracies with faster convergence, but in the case of the non-convex optimization problems, momentum optimizers will not work well if we still tune the decay factor. To solve the problem of non-convex optimizations, Nesterov accelerated ingredients were introduced which was an improved or upgraded version of momentum optimizers with faster convergence on non-convex and convex optimization problems. In short, NAG is an optimization technique that is similar to momentum optimization but the only change is there are fewer epochs needed than momentum optimizers to converge the solution of the problem.

The Mathematics Behind Nag

In the case of the normal gradient descent optimization technique, the formula for weight update is

Wnew = Wold - n (dL/dW)

Where,

Wnew = The new updated weight

Wold = Old weight, which is to be updated

n = learning rate

dL/dW = derivative of loss with respect to weight

In the case of the momentum optimization function, the formula would be

Image Source

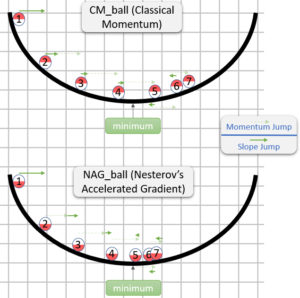
Here the weight update will happen with momentum, where the oscillations of epochs need to converge to the solution can be reduced by tuning the decay factor (Y). So here the new weight would be the value obtained from the velocity term subtracted from the old weight. where the velocity term is the form that provides momentum to the optimizer. In momentum gradient which is the sum of two terms past velocity and gradient at a particular point. So here in the graph of loss vs weights, the path of the point on the gradient will be decided by these two terms. Basically here there will be longer jumps as there are two terms the normal gradients value and the past velocity push from the point. So by wicking the formula of momentum gradient, we can easily achieve the Nesterov gradient, basically, the main difference in these two optimizers is just an update from where it will be calculated. In momentum, the update of the weight is basically calculated with two terms, momentum t that point and past velocity at a single time, but in the case of Nesterov accelerated gradient the weight update is calculated stepwise, basically the weight update will occur first according to the history of velocity and then the gradient at that particular point in step 2. So basically, in momentum both of the steps will occur simultaneously whereas in the Nesterov gradient both of the steps will occur step by step and because of this the Nesterov accelerated gradient always performs better than the momentum gradient optimization technique. The formula for the NAG optimizer is

Image Source

As we can see in the formula of the Nesterov gradient, the weight update will occur according to acceleration and the formula for final weight update represents an accelerated term which is a stepwise execution of the history velocity term and the gradient at a particular point. The update formula is very similar to the momentum term, just an additional term of look ahead. look ahead is a term that represents the point where we will reach after the jump from the momentum term. mathematically the look ahead term is a term that is obtained by the substation of old weight and the momentum after the first jump.

Why Nag is Faster?

In the case of the momentum optimization technique, the jump or weight update occur as a result of 2 terms with a single step which is the history of the momentum term and normal gradient at a particular point. Due to this we will surely cross the minima point and will reach the other side of the minima, again there will be a need for some more epochs to come back to the minima point. But in the case of the Nesterov gradient optimization technique, the weight update will occur in two steps, in the first step the weight update will occur due to the history of momentum and in the second step, the weight update will occur due to the look-ahead term. So here the minima point will not be crossed and there will be a need for less number of epochs, which will make training fast.

Image Source

Implementation of Nag: Code

There is not any specific class in Keras to implement NAG Optimiser but we can use the Nesterov parameter by using the parameters available in other optimizers.

For example if you want to implement NAG Optimiser in stochastic Gradient descent then there are parameters in it using which NAG can be implemented.

To implement NAG in SGD, Use the parameter named as “Nesterov”, and pass the value True in it, by doing this the NAG will be automatically implemented in SGD.

Code Example:

# Without Nag
tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=False, name="SGD", **kwargs
)

# With Nag
tf.keras.optimizers.SGD(
    learning_rate=0.01, momentum=0.0, nesterov=True, name="SGD", **kwargs
)

Conclusion

In this article, the basic idea of optimizers in deep learning is discussed. momentum and Nesterov accelerated gradient optimizers are discussed with the core intuition and mathematical formulations. The main reason behind the faster convergence of NAG optimizer is discussed with the mathematical formulations and discussions.

Some Key Takeaways from this article are:

  1. Momentum optimization is a faster optimization technique than normal gradient descent with the concept of momentum applying.
  2. Nesterov accelerated gradient is an optimization technique that is developed to solve the slower convergence of momentum optimizers as weight update occur with 2 terms history velocity and gradient at a point in a single step.
  3. The Nesterov accelerated gradient ar the faster convergence optimizer with stepwise weight update of history velocity and look ahead velocity.

References

  • [1] https://keras.io/api/optimizers/
  • [2] https://www.nag.com/content/mathematical-optimization-software
  • [3] https://towardsdatascience.com/optimizers-for-training-neural-network-59450d71caf6
  • [4] https://jlmelville.github.io/mize/nesterov.html
  • [5] https://ruder.io/optimizing-gradient-descent/